keras之regression实现
导入库
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf
from tensorflow import keras
# 查看当前版本号
print(tf.__version__)
print(sys.version_info)
for module in mpl, np, pd, sklearn, tf, keras:
print(module.__name__, module.__version__)2.0.0-alpha0
sys.version_info(major=3, minor=6, micro=13, releaselevel='final', serial=0)
matplotlib 3.3.4
numpy 1.16.2
pandas 1.1.5
sklearn 0.24.1
tensorflow 2.0.0-alpha0
tensorflow.python.keras.api._v2.keras 2.2.4-tf
# 直接从skleranCalifornia housing的数据
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing(data_home="datasets/mldata", download_if_missing=True)
print(housing.DESCR).. _california_housing_dataset:
California Housing dataset
--------------------------
**Data Set Characteristics:**
:Number of Instances: 20640
:Number of Attributes: 8 numeric, predictive attributes and the target
:Attribute Information:
- MedInc median income in block
- HouseAge median house age in block
- AveRooms average number of rooms
- AveBedrms average number of bedrooms
- Population block population
- AveOccup average house occupancy
- Latitude house block latitude
- Longitude house block longitude
:Missing Attribute Values: None
This dataset was obtained from the StatLib repository.
http://lib.stat.cmu.edu/datasets/
The target variable is the median house value for California districts.
This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).
It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.
.. topic:: References
- Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
Statistics and Probability Letters, 33 (1997) 291-297
# 看下维度
print(housing.data.shape)
print(housing.target.shape)(20640, 8)
(20640,)
print(housing.data[0])[ 8.3252 41. 6.98412698 1.02380952 322.
2.55555556 37.88 -122.23 ]
import pprint
pprint.pprint(housing.data[0:5])
pprint.pprint(housing.target[0:5])array([[ 8.32520000e+00, 4.10000000e+01, 6.98412698e+00,
1.02380952e+00, 3.22000000e+02, 2.55555556e+00,
3.78800000e+01, -1.22230000e+02],
[ 8.30140000e+00, 2.10000000e+01, 6.23813708e+00,
9.71880492e-01, 2.40100000e+03, 2.10984183e+00,
3.78600000e+01, -1.22220000e+02],
[ 7.25740000e+00, 5.20000000e+01, 8.28813559e+00,
1.07344633e+00, 4.96000000e+02, 2.80225989e+00,
3.78500000e+01, -1.22240000e+02],
[ 5.64310000e+00, 5.20000000e+01, 5.81735160e+00,
1.07305936e+00, 5.58000000e+02, 2.54794521e+00,
3.78500000e+01, -1.22250000e+02],
[ 3.84620000e+00, 5.20000000e+01, 6.28185328e+00,
1.08108108e+00, 5.65000000e+02, 2.18146718e+00,
3.78500000e+01, -1.22250000e+02]])
array([4.526, 3.585, 3.521, 3.413, 3.422])
拆分训练集,测试集和验证集
from sklearn.model_selection import train_test_split
x_train_all, x_test, y_train_all, y_test = train_test_split(
housing.data, housing.target, random_state = 7)
x_train, x_valid, y_train, y_valid = train_test_split(
x_train_all, y_train_all, random_state = 11)
print(x_train.shape, y_train.shape)
print(x_valid.shape, y_valid.shape)
print(x_test.shape, y_test.shape)(11610, 8) (11610,)
(3870, 8) (3870,)
(5160, 8) (5160,)
归一化数据集
概率模型(树形模型)不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、RF。而像Adaboost、SVM、LR、Knn、KMeans之类的最优化问题就需要归一化。
- fit(): Method calculates the parameters μ and σ and saves them as internal objects.
解释:简单来说,就是求得训练集X的均值,方差,最大值,最小值,这些训练集X固有的属性。
- transform(): Method using these calculated parameters apply the transformation to a particular dataset.
解释:在fit的基础上,进行标准化,降维,归一化等操作(看具体用的是哪个工具,如PCA,StandardScaler等)。
- fit_transform(): joins the fit() and transform() method for transformation of dataset.
解释:fit_transform是fit和transform的组合,既包括了训练又包含了转换。
transform()和fit_transform()二者的功能都是对数据进行某种统一处理(比如标准化~N(0,1),将数据缩放(映射)到某个固定区间,归一化,正则化等)
- fit_transform(trainData)对部分数据先拟合fit,找到该part的整体指标,如均值、方差、最大值最小值等等(根据具体转换的目的),然后对该trainData进行转换transform,从而实现数据的标准化、归一化等等。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_valid_scaled = scaler.transform(x_valid)
x_test_scaled = scaler.transform(x_test)print(x_train_scaled[0])
print(x_train[0])[ 0.80154431 0.27216142 -0.11624393 -0.20231151 -0.54305157 -0.02103962
-0.58976206 -0.08241846]
[ 5.345 32. 5.13541667 0.99652778 830.
2.88194444 34.38 -119.74 ]
构建模型
- Sequential 模型结构: 层(layers)的线性堆栈。简单来说,它是一个简单的线性结构,没有多余分支,是多个网络层的堆叠。
# tf.keras.layers.Dense(
# inputs=64, # 输入该网络层的数据
# units=10, # 输出的维度大小
# activation=None, # 选择使用的(激活函数)
# use_bias=True, # 是否使用(偏置项)
# kernel_initializer=None, # 卷积核的初始化器
# bias_initializer=tf.zeros_initializer(), # 偏置项的初始化器
# kernel_regularizer=None, # 卷积核的正则化
# activaty_regularizer=None, # 偏置项的正则化
# kernel_constraint=None, # 对主权重矩阵进行约束
# bias_constraint=None, # 对偏置向量进行约束
# trainable=True, # 可以设置为不可训练,(冻结)网络层
# name=None, # 层的名字
# reuse=None # 是否重复使用参数
# )# ReLu的使用,使得网络可以自行引入稀疏性
model = keras.models.Sequential([
keras.layers.Dense(30, activation='relu',
input_shape=x_train.shape[1:]),
keras.layers.Dense(1),
])
model.summary()Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_2 (Dense) (None, 30) 270
_________________________________________________________________
dense_3 (Dense) (None, 1) 31
=================================================================
Total params: 301
Trainable params: 301
Non-trainable params: 0
_________________________________________________________________
# optimizer可以是字符串形式给出的优化器名字,也可以是函数形式,使用函数形式可以设置学习率、动量和超参数
# 例如:“sgd” 或者 tf.optimizers.SGD(lr = 学习率, decay = 学习率衰减率, momentum = 动量参数)
# adagrad" 或者 tf.keras.optimizers.Adagrad(lr = 学习率,decay = 学习率衰减率)
# adadelta" 或者 tf.keras.optimizers.Adadelta(lr = 学习率, decay = 学习率衰减率)
# adam" 或者 tf.keras.optimizers.Adam(lr = 学习率, decay = 学习率衰减率)
# loss可以是字符串形式给出的损失函数的名字,也可以是函数形式
# 例如:”mse" 或者 tf.keras.losses.MeanSquaredError()
# sparse_categorical_crossentropy" 或者 tf.keras.losses.SparseCatagoricalCrossentropy(from_logits = False)
# 损失函数经常需要使用softmax函数来将输出转化为概率分布的形式,在这里from_logits代表是否将输出转为概率分布的形式,为False时表示转换为概率分布,为True时表示不转换,直接输出
# Metrics标注网络评价指标
# 例如:
# "accuracy" : y_ 和 y 都是数值,如y_ = [1] y = [1] #y_为真实值,y为预测值
# “sparse_accuracy":y_和y都是以独热码 和概率分布表示,如y_ = [0, 1, 0], y = [0.256, 0.695, 0.048]
# "sparse_categorical_accuracy" :y_是以数值形式给出,y是以 独热码给出,如y_ = [1], y = [0.256 0.695, 0.048]# model.compile()方法用于在配置训练方法时,告知训练时用的优化器、损失函数和准确率评测标准
model.compile(loss="mean_squared_error", optimizer="sgd")回调
回调是传递给模型以自定义和扩展其在训练期间的行为的对象。我们可以编写自己的自定义回调,或使用tf.keras.callbacks中的内置函数,常用内置回调函数如下:
- tf.keras.callbacks.ModelCheckpoint:定期保存模型的检查点。
- tf.keras.callbacks.LearningRateScheduler:动态更改学习率。
- tf.keras.callbacks.EarlyStopping:验证性能停止提高时进行中断培训。
- tf.keras.callbacks.TensorBoard:使用TensorBoard监视模型的行为 。
# EarlyStopping是什么
# EarlyStopping是Callbacks的一种,callbacks用于指定在每个epoch开始和结束的时候进行哪种特定操作。Callbacks中有一些设置好的接口,可以直接使用,如’acc’,’val_acc’,’loss’和’val_loss’等等。
# EarlyStopping则是用于提前停止训练的callbacks。具体地,可以达到当训练集上的loss不在减小(即减小的程度小于某个阈值)的时候停止继续训练。
# 为什么要用EarlyStopping
# 根本原因就是因为继续训练会导致测试集上的准确率下降。
# 那继续训练导致测试准确率下降的原因猜测可能是1. 过拟合 2. 学习率过大导致不收敛 3. 使用正则项的时候,Loss的减少可能不是因为准确率增加导致的,而是因为权重大小的降低。
# 当然使用EarlyStopping也可以加快学习的速度,提高调参效率。
callbacks = [keras.callbacks.EarlyStopping(
patience=5, min_delta=1e-2)]训练
history = model.fit(x_train_scaled, y_train,
validation_data = (x_valid_scaled, y_valid),
epochs = 50,
callbacks = callbacks)Train on 11610 samples, validate on 3870 samples
Epoch 1/50
11610/11610 [==============================] - 0s 40us/sample - loss: 2.1284 - val_loss: 0.9146
Epoch 2/50
11610/11610 [==============================] - 0s 30us/sample - loss: 0.7530 - val_loss: 0.7634
Epoch 3/50
11610/11610 [==============================] - 0s 31us/sample - loss: 0.6862 - val_loss: 0.7277
Epoch 4/50
11610/11610 [==============================] - 0s 25us/sample - loss: 0.6552 - val_loss: 0.6985
Epoch 5/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.6312 - val_loss: 0.6747
Epoch 6/50
11610/11610 [==============================] - 0s 26us/sample - loss: 0.6099 - val_loss: 0.6523
Epoch 7/50
11610/11610 [==============================] - 0s 26us/sample - loss: 0.5930 - val_loss: 0.6347
Epoch 8/50
11610/11610 [==============================] - 0s 31us/sample - loss: 0.5773 - val_loss: 0.6172
Epoch 9/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.5636 - val_loss: 0.6025
Epoch 10/50
11610/11610 [==============================] - 0s 27us/sample - loss: 0.5514 - val_loss: 0.5897
Epoch 11/50
11610/11610 [==============================] - 0s 27us/sample - loss: 0.5403 - val_loss: 0.5771
Epoch 12/50
11610/11610 [==============================] - 0s 29us/sample - loss: 0.5310 - val_loss: 0.5667
Epoch 13/50
11610/11610 [==============================] - 0s 25us/sample - loss: 0.5221 - val_loss: 0.5570
Epoch 14/50
11610/11610 [==============================] - 0s 30us/sample - loss: 0.5147 - val_loss: 0.5485
Epoch 15/50
11610/11610 [==============================] - 0s 26us/sample - loss: 0.5078 - val_loss: 0.5405
Epoch 16/50
11610/11610 [==============================] - 0s 27us/sample - loss: 0.5016 - val_loss: 0.5329
Epoch 17/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.4958 - val_loss: 0.5266
Epoch 18/50
11610/11610 [==============================] - 0s 31us/sample - loss: 0.4910 - val_loss: 0.5213
Epoch 19/50
11610/11610 [==============================] - 0s 30us/sample - loss: 0.4863 - val_loss: 0.5155
Epoch 20/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.4819 - val_loss: 0.5096
Epoch 21/50
11610/11610 [==============================] - 0s 29us/sample - loss: 0.4784 - val_loss: 0.5055
Epoch 22/50
11610/11610 [==============================] - 0s 32us/sample - loss: 0.4746 - val_loss: 0.5019
Epoch 23/50
11610/11610 [==============================] - 0s 25us/sample - loss: 0.4712 - val_loss: 0.4969
Epoch 24/50
11610/11610 [==============================] - 0s 27us/sample - loss: 0.4680 - val_loss: 0.4941
Epoch 25/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.4655 - val_loss: 0.4907
Epoch 26/50
11610/11610 [==============================] - 0s 29us/sample - loss: 0.4625 - val_loss: 0.4882
Epoch 27/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.4599 - val_loss: 0.4854
Epoch 28/50
11610/11610 [==============================] - 0s 30us/sample - loss: 0.4575 - val_loss: 0.4814
Epoch 29/50
11610/11610 [==============================] - 0s 30us/sample - loss: 0.4549 - val_loss: 0.4811
Epoch 30/50
11610/11610 [==============================] - 0s 27us/sample - loss: 0.4528 - val_loss: 0.4764
Epoch 31/50
11610/11610 [==============================] - 0s 29us/sample - loss: 0.4506 - val_loss: 0.4737
Epoch 32/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.4487 - val_loss: 0.4726
Epoch 33/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.4468 - val_loss: 0.4700
Epoch 34/50
11610/11610 [==============================] - 0s 28us/sample - loss: 0.4447 - val_loss: 0.4670
Epoch 35/50
11610/11610 [==============================] - 0s 30us/sample - loss: 0.4432 - val_loss: 0.4650
Epoch 36/50
11610/11610 [==============================] - 0s 27us/sample - loss: 0.4412 - val_loss: 0.4638
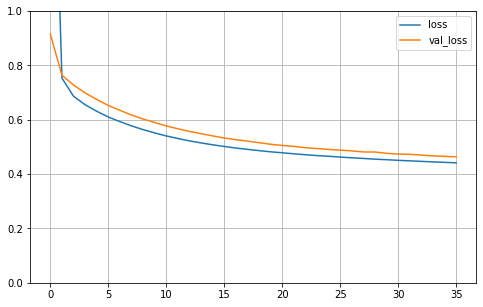
看下训练的走向
def plot_learning_curves(history):
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1)
plt.show()
plot_learning_curves(history) 
model.evaluate(x_test_scaled, y_test)5160/5160 [==============================] - 0s 16us/sample - loss: 0.4583
0.4583061384600262
结果只有45%